What are embeddings?
Embeddings are mathematical representations that capture the essence of data in a lower-dimensional space. In the context of AI, embeddings typically refer to dense vectors that represent entities, be it words, products, or even users.
For our E-commerce use case, where our product catalog is made up of bags, here's what the numerical representation of a bag might look like:

Encoding Socks and Shoes
This illustration shows how distinct items, such as a sock and a shoe, are converted into numerical form using an embedding model. Each item is represented by a dense 300-dimensional vector, a compact array of real numbers, where each element encodes some aspect of the item's characteristics.
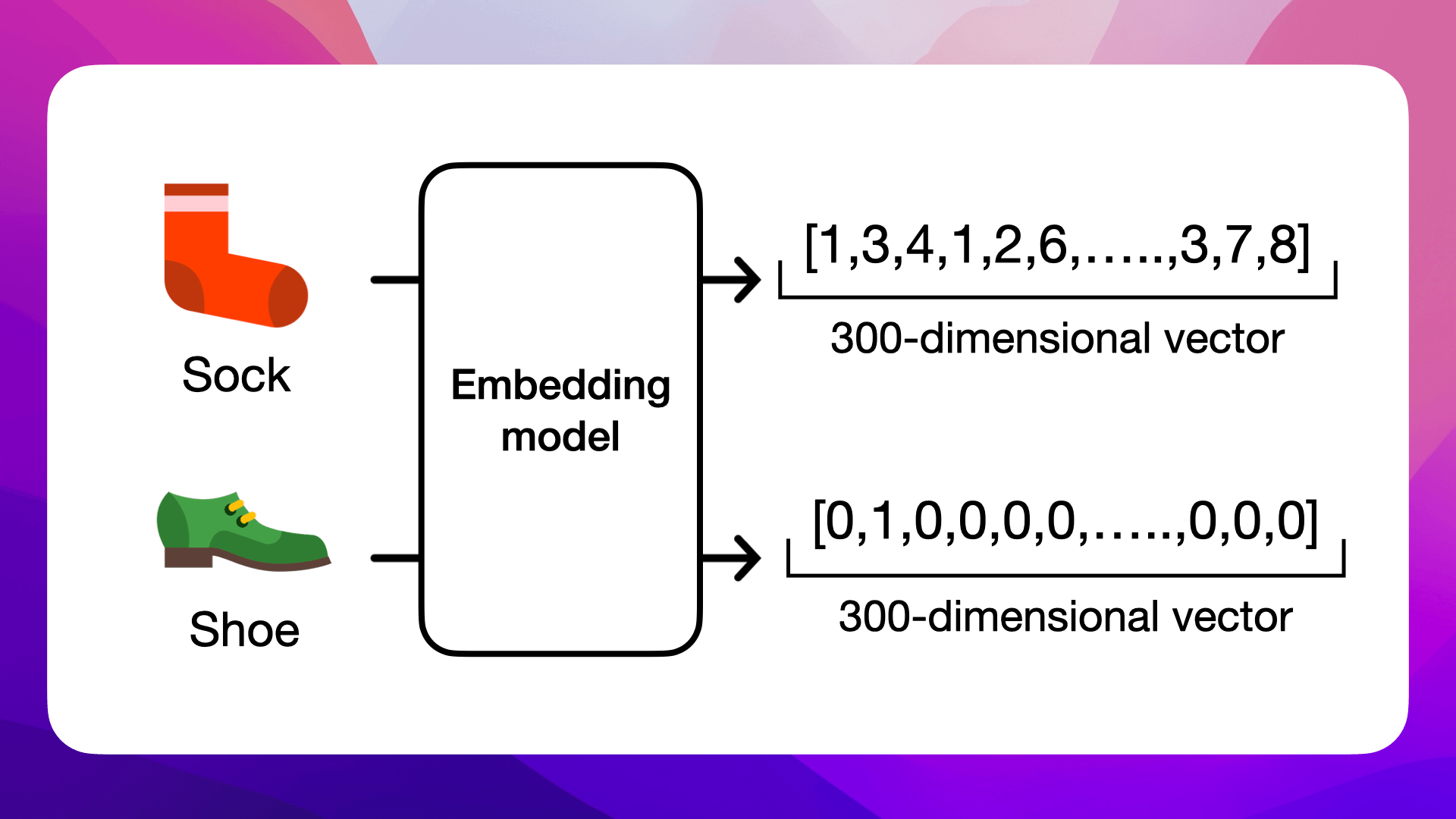
These vectors allow AI models to grasp and quantify the subtle semantic relationships between different items. For instance, the embedding for a sock is likely to be closer in vector space to a shoe than to unrelated items, reflecting their contextual relationship in the real world. This transformation is central to AI's ability to process and analyze vast amounts of complex data efficiently.
The beauty of embeddings
The beauty of embeddings lies in their ability to capture semantic relationships; for instance, embeddings of the words sock and shoe might be closer to each other than sock and apple.
Dense vs. Sparse Vectors
To understand embeddings more fully, it's important to distinguish between dense and sparse vectors, two fundamental types of vector representations in AI.
Dense Vectors
Dense vectors are compact arrays where every element is a real number, often generated by algorithms like word embeddings. These vectors have a fixed size, and each dimension within them carries some information about the data point. In embeddings, dense vectors are preferable as they can efficiently capture complex relationships and patterns in a relatively lower-dimensional space.

Sparse Vectors
Conversely, sparse vectors are typically high-dimensional and consist mainly of zeros or null values, with only a few non-zero elements. These vectors often arise in scenarios like one-hot encoding, where each dimension corresponds to a specific feature of the dataset (e.g., the presence of a word in a text). Sparse vectors can be very large and less efficient in terms of storage and computation, but they are straightforward to interpret.
The transition from sparse to dense vectors, as in the case of embeddings, is a key aspect of reducing dimensionality and extracting meaningful patterns from the data, which can lead to more effective and computationally efficient models.

Transitioning from sparse to dense vectors is essential in AI for reducing dimensionality and capturing meaningful data patterns.
How Embeddings Relate to Vector Space
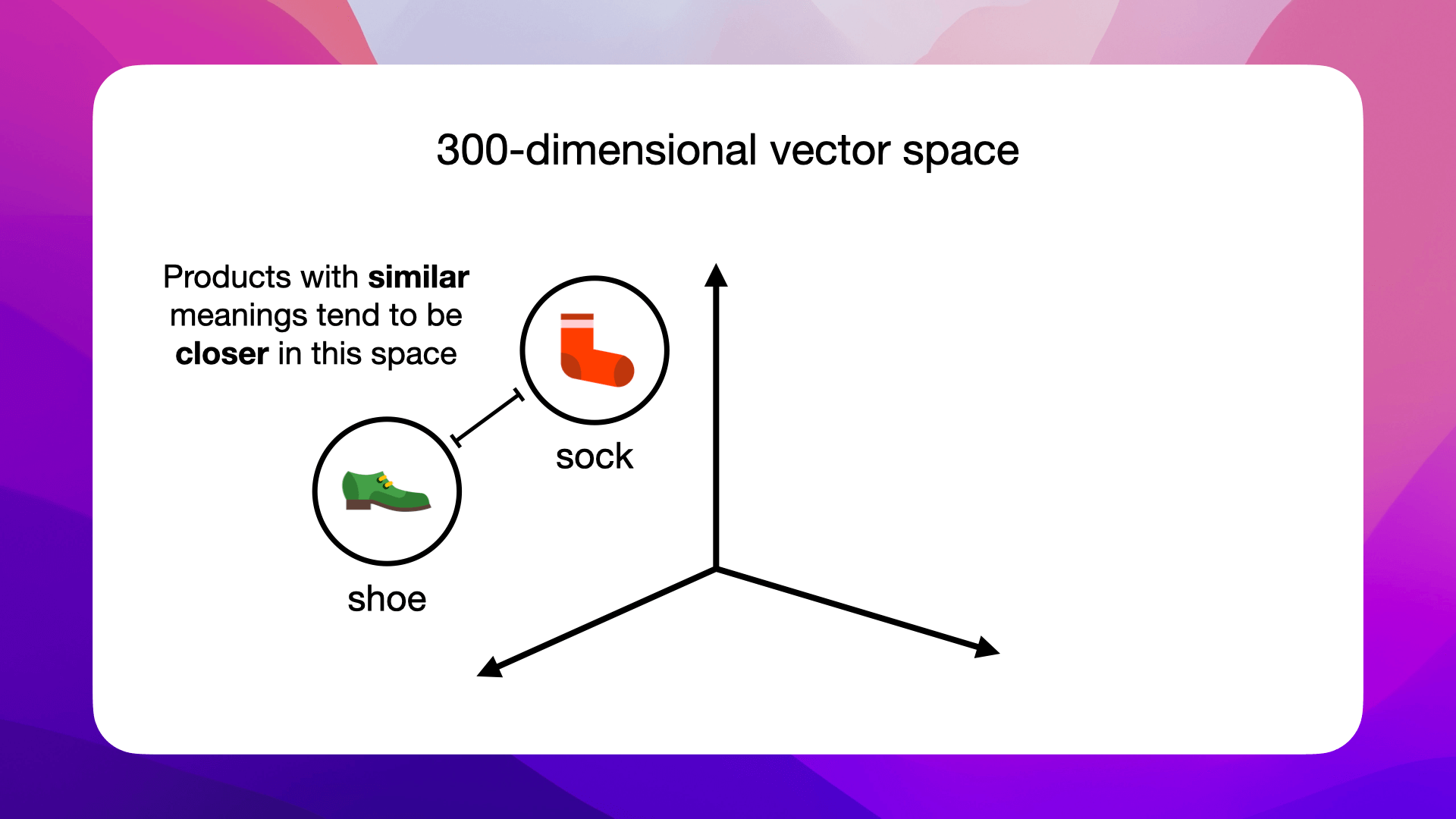
Every embedding resides in a vector space. The dimensions of this space depend on the size of the embeddings. For example, a 300-dimensional word embedding for the word "sock" belongs to a 300-dimensional vector space:

The position of an embedding within this space carries semantic meaning. Entities with similar meanings or functions tend to be closer in this space, like shoes and socks:
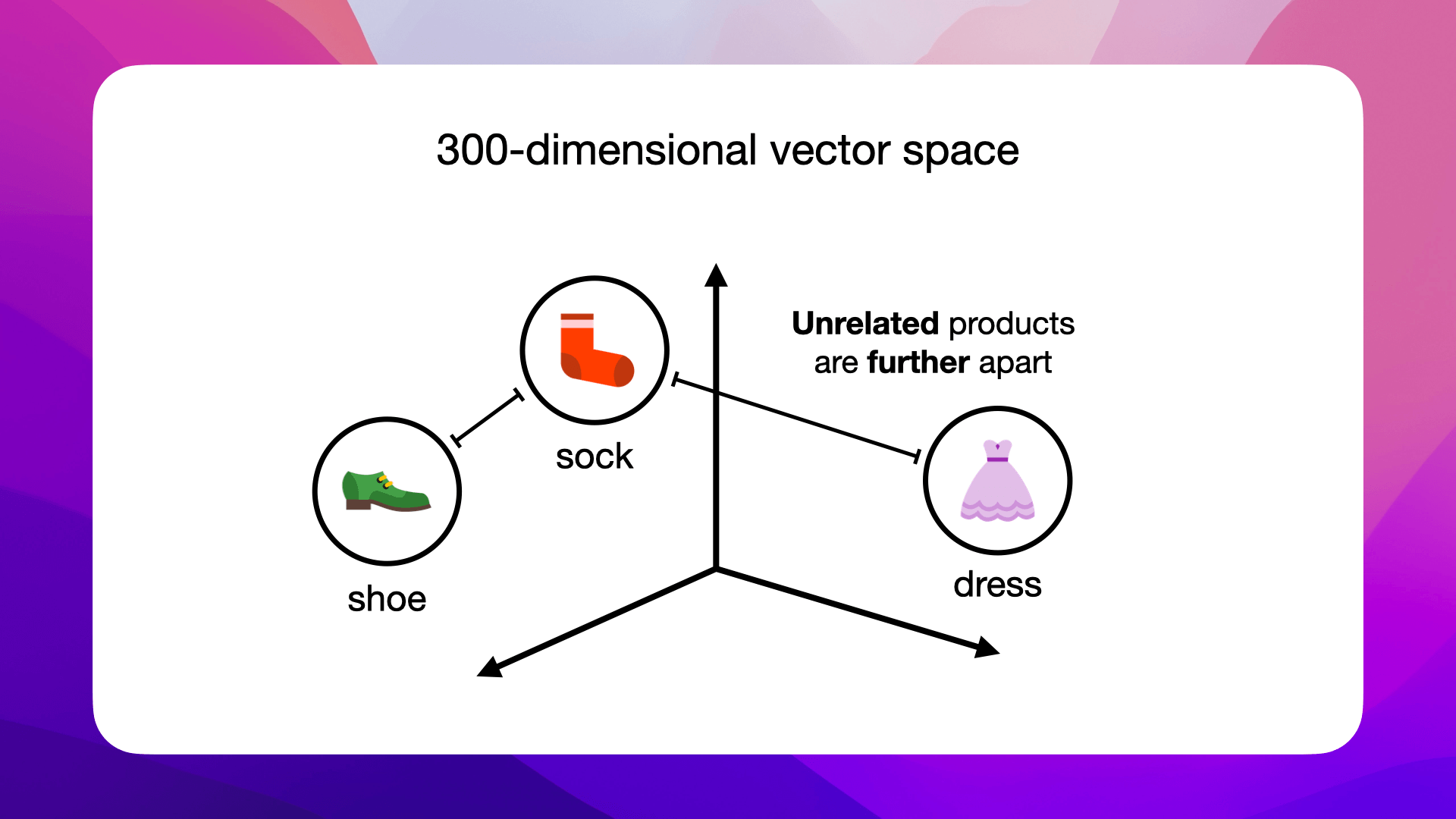
While unrelated ones, like sock and dress, are further apart:
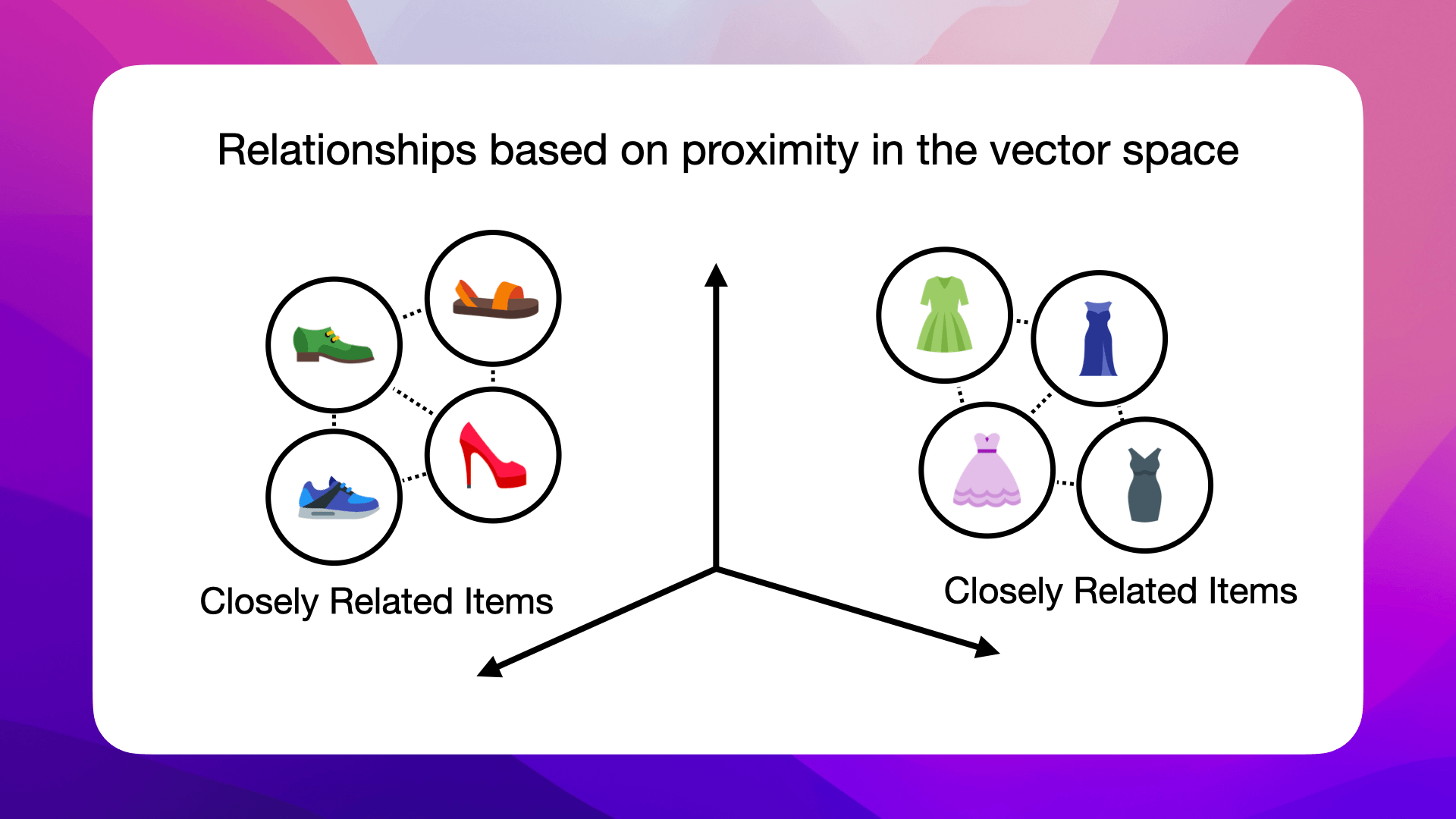
This spatial relation makes embeddings powerful: they allow algorithms to infer relationships based on proximity in the vector space:

Now that we know what embeddings are, let's look at how we can compare and measure the similarities between one of your products and what a customer is asking about, in the next section.